Term SOFR and Treasury Forward Curves
The Term SOFR forward curves represent market-implied future settings for 1-month and 3-month Term SOFR, index rates commonly used in floating rate commercial real estate and corporate financings. The Treasury forward curves represent market-implied future yields of on-the-run U.S. Treasury notes of different tenors. Each curve is derived from observable market data, including futures contracts, market swap rates, and current outstanding Treasury instruments. Forward curves are often useful for forecasting and underwriting floating- and fixed-rate debt or for calculating yield maintenance but should not be viewed as predictive of actual future interest rates. Contact us to speak with an expert.
Currently showing:
Informational Purposes Only - Disclaimer | Terms of use
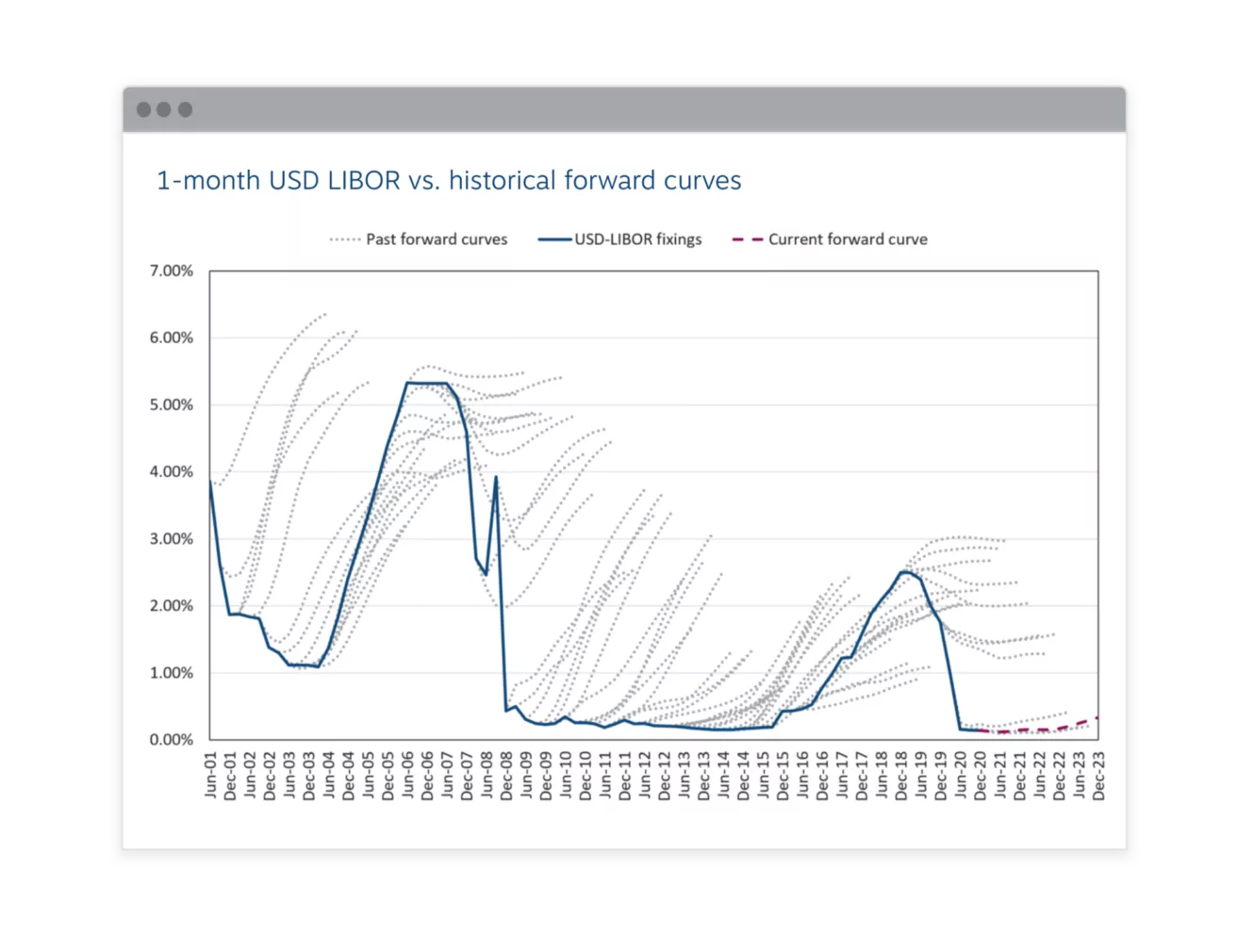
See how past forward curve projections have stacked up
Review our "hairy charts" for an analysis showing 1-month USD LIBOR, 3-month GBP LIBOR, and 3-month EURIBOR forward curves versus actual rate fixings over time.
Market Rates and Calculators
-
U.S. Market Rates
Current and historical US swap rates, treasury yields, Fallback Rate (SOFR), SOFR, Term SOFR swap rates, SIFMA, Fed Funds, Prime, and other interest rate risk benchmarks.
-
Interest Rate Cap Calculator
Estimate your costs of hedging floating rate debt with Chatham's interest rate cap pricing calculator. Simply enter the notional amount, term, and cap strike price for indicative pricing.
-
Defeasance Calculator
Get an estimated defeasance cost in minutes with Chatham's free and confidential defeasance calculator – no email address required.
-
Yield Maintenance Calculator
Estimating your prepayment costs is quick and easy with Chatham's free yield maintenance calculator – get an estimate in minutes with no email address required.
-
FX Rates
Check current and historical foreign exchange rates for some of the most heavily traded currency pairs in the world including EUR-USD, GBP-USD, and more.
-
European Market Rates
View current and historical rates EURIBOR, SONIA, and Gilt indices plus EURIBOR, SONIA, STIBOR, CIBOR, NIBOR, WIBOR, and PRIBOR swap rates.
Our featured insights
Our team
Get in touch with an expert
Need live rates or have general questions? We advise on and execute over $4.5 billion per trading day of interest rate and FX hedging transactions.
Disclaimers
Chatham Hedging Advisors, LLC (CHA) is a subsidiary of Chatham Financial Corp. and provides hedge advisory, accounting and execution services related to swap transactions in the United States. CHA is registered with the Commodity Futures Trading Commission (CFTC) as a commodity trading advisor and is a member of the National Futures Association (NFA); however, neither the CFTC nor the NFA have passed upon the merits of participating in any advisory services offered by CHA. For further information, please visit chathamfinancial.com/legal-notices.
Transactions in over-the-counter derivatives (or “swaps”) have significant risks, including, but not limited to, substantial risk of loss. You should consult your own business, legal, tax and accounting advisers with respect to proposed swap transaction and you should refrain from entering into any swap transaction unless you have fully understood the terms and risks of the transaction, including the extent of your potential risk of loss. This material has been prepared by a sales or trading employee or agent of Chatham Hedging Advisors and could be deemed a solicitation for entering into a derivatives transaction. This material is not a research report prepared by Chatham Hedging Advisors. If you are not an experienced user of the derivatives markets, capable of making independent trading decisions, then you should not rely solely on this communication in making trading decisions. All rights reserved.
23-0081ICE BENCHMARK ADMINISTRATION LIMITED MAKES NO WARRANTY, EXPRESS OR IMPLIED, EITHER AS TO THE RESULTS TO BE OBTAINED FROM THE USE OF ICE LIBOR AND/OR THE FIGURE AT WHICH ICE LIBOR STANDS AT ANY PARTICULAR TIME ON ANY PARTICULAR DAY OR OTHERWISE. ICE BENCHMARK ADMINISTRATION LIMITED MAKES NO EXPRESS OR IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE IN RESPECT OF ANY USE OF ICE LIBOR.











